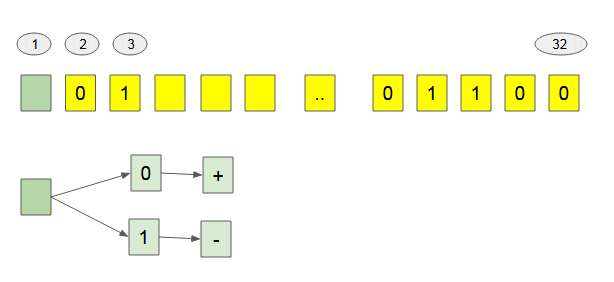
Bitwise Operations

Bitwise
Bitwise operation on numbers
What is Bitwise used for?

1. Bitwise

In digital computer programming. The bitwise operation works on one or more binary numerals, or binary numerals-like strings. This is a simple and fast operation, directly supported by processor. Normally, bitwise operations are much faster than multiplication, division, sometimes significantly faster than addition. bitwise calculations use less energy because it rarely uses resources.

There are 7 bitwise operations :

Operator	Name	Description
&	AND	If both bits are 1, the return value is 1, otherwise it returns 0.
\|	OR	If one of two bits is 1, the return value is 1, otherwise it returns 0.
^	XOR	If 2 bits are different, the return value is 1, otherwise it returns 0.
~	NOT	Inverts all the bits, 0 to 1 and 1 to 0.
<<	Zero fill left shift	Shifts all bits to the left.
>>	Signed right shift	Shifts all bits to the right except the first bit.
>>>	Zero fill right shift	Shifts all bits to the right.

Bitwise AND

When a bitwise AND is performed on a pair of bits, it returns 1 if both bits are 1, otherwise returns 0.

Example with 1 bit:

Operation	Result
0 & 0	0
0 & 1	0
1 & 0	0
1 & 1	1

Example with 4 bit:

Operation	Result
1111 & 0000	0000
1111 & 0001	0001
1111 & 0010	0010
1111 & 0100	0100

Bitwise OR:

When a bitwise OR is performed on a pair of bits, it returns 1 if one of the bits are 1, otherwise returns 0.

Example with 1 bit:

Operation	Result
0 \| 0	0
0 \| 1	1
1 \| 0	1
1 \| 1	1

Example with 4 bits:

Operation	Result
1111 \| 0000	1111
1111 \| 0001	1111
1111 \| 0010	1111
1111 \| 0100	1111

Bitwise XOR

When a bitwise XOR is performed on a pair of bits, it returns 1 if the bits are different, otherwise returns 0.

Example with 1 bit:

Operation	Result
0 ^ 0	0
0 ^ 1	1
1 ^ 0	1
1 ^ 1	0

Example with 4 bits:

Operation	Result
1111 ^ 0000	1111
1111 ^ 0001	1110
1111 ^ 0010	1101
1111 ^ 0100	1011

Bitwise NOT

When a Bitwise NOT is used, it will reverse all bits, 1 to 0, and 0 to 1.

Example with 1 bit:

Operation	Result
~ 0	1
~ 1	0

Example with 4 bits:

Operation	Result
~ 0000	1111
~ 0001	0001
~ 0010	1101
~ 1100	0011

2. Bitwise operation on numbers

Different languages can have multiple data types to represent numbers.

Java: byte, short, int, long, double.
C#:byte, sbyte, short, ushort, int, uint, long, ulong, float, double
Javascript: double
.....

Javascript stores numbers as 64 bits floating point numbers. But bitwise operations are performed on 32-bit integers. Other languages such as Java, C#,.. bitwise operations are also performed on 32-bit integers.

Therefore, before carrying out the bitwise operations with numbers, you have to convert each number into a sequence of 32 binary numbers.

Base 10	Base 2	32 bits
5	101	00000000000000000000000000000101
218	11011010	00000000000000000000000011011010

In Javascript, the toString(base) method helps you change any number from base 10 to other base.

toString-base-example.js (Javascript)

let a = 8; 
// Base 2 string.
console.log( a.toString(2) );// 1000

// Base 8 string
console.log( a.toString(8) ); // 10

// Base 16 string
console.log( a.toString(16) ); // 8

let b = 218; 
// Base 2 string.
console.log( b.toString(2) );// 11011010

// Base 8 string
console.log( b.toString(8) ); // 332

// Base 16 string
console.log( b.toString(16) ); // da

Example:

Decimal	Binary
5	00000000000000000000000000000101
1	00000000000000000000000000000001
5 & 1 = 1	00000000000000000000000000000001
5 \| 1 = 5	00000000000000000000000000000101
5 ^ 1 = 4	00000000000000000000000000000100
~ 5 = -6	11111111111111111111111111111010

Note: Of 32 bits, the first bit is used to determine the sign of number. If this bit is 1, it corresponds to the ( - ) sign. If this bit is 0 , it corresponds to the ( + ) sign
History of bits and bytes in computer science

Bitwise Left Shift (<<)

Decimal	Binary
5	00000000000000000000000000000101
5 << 1 = 10	00000000000000000000000000001010
5 << 2 = 20	00000000000000000000000000010100

The Bitwise Left Shift ( << ) Operator can change the sign of number.

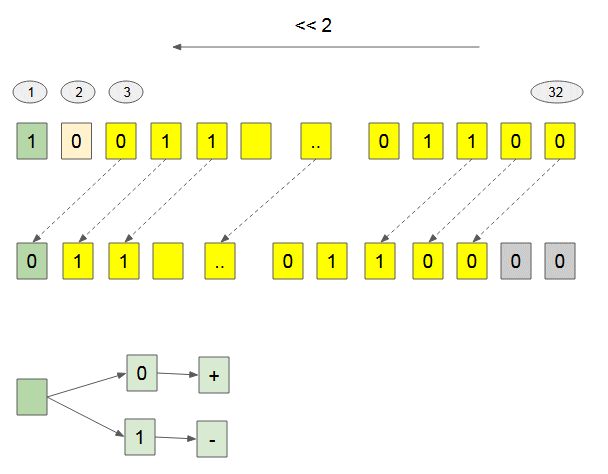
(Javascript code)

console.log( 1073741824 << 1); // -2147483648
console.log( 2684354560 << 1); // 1073741824

Bitwise Right Shift (>>) [Unsigned Right Shift]

Decimal	Binary
29	00000000000000000000000000011101
29 >> 1 = 14	00000000000000000000000000001110
29 >> 2 = 7	00000000000000000000000000000111

The Bitwise Right Shift ( >> ) operator doesn't change the sign of number because the first bit is not moved.

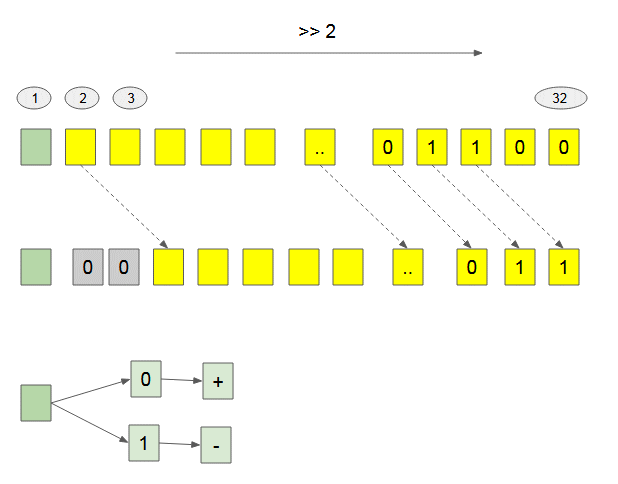
Bitwise Right Shift (>>>) [Zero fill right Shift]

The Bitwise Right Shift ( >>> ) operator can change the number sign.

(Javascript Code)

console.log( -1073741824 >>> 1); // 1610612736
console.log( 1073741824 >>> 1); // 536870912

3. What is Bitwise used for?

The bitwise calculations are directly supported by the computer processor, it performs very fast. Below, I list some examples of using these calculations.

Use the bitwise operations on Strings (characters) in the Java, C#, C/C++ ...languages. Note: some languages such as Javascript don't support the bitwise operation with String type.

Convert an Uppercase into Lowercase:

// Rule: x | ' '

('A' | ' ') ==> 'a'
('B' | ' ') ==> 'b'

('a' | ' ') => 'a'

Convert Lowercase into Uppercase:

// Rule: x & '_'

('a' & '_') ==> 'A'
('b' & '_') ==> 'B'
('A' & '_') ==> 'A'

Reverse uppercase to lowercase, lowercase to uppercase:

// Rule: x ^ ' '

('a' ^ ' ') ==> 'A'
('A' ^ ' ') ==> 'a'

View the position of Latin letters (applying to only uppercase)

// Rule:  x & '?'
'A' & '?'  ==> 1
'B' & '?'  ==> 2
...
'Z' & '?'  ==> 26

// Rule:  x ^ '@' 
'A' ^ '@'  ==> 1
'B' ^ '@'  ==> 2
...
'Z' ^ '@'  ==> 26

View the position of Latin letters (applying only to lowercase)

// Rule:  x ^ '`' 
'a' ^ '`'  ==> 1
'b' ^ '`'  ==> 2
...
'z' ^ '`'  ==> 26
// '`' : binary ( 1100000 ), hex('60'),  chr(96)

View the position of Latin letters, applying to both uppercase and lowercase:

// Rule:  x & '\u001F' 
'A' & '\u001F'  ==> 1
'B' & '\u001F'  ==> 2
...
'Z' & '\u001F'  ==> 26

'A' & '\u001F'  ==> 1
'B' & '\u001F'  ==> 2
...
'Z' & '\u001F'  ==> 26

Operation	Result
0 \| 0	0
0 \| 1	1
1 \| 0	1
1 \| 1	1

Bitwise Operations

1. Bitwise

2. Bitwise operation on numbers

3. What is Bitwise used for?

ECMAScript, Javascript Tutorials

Java Basic

ECMAScript, Javascript Tutorials

Java Basic

Newest Articles