o7planning

History of bits and bytes in computer science

  1. Bit
  2. Byte

1. Bit

I start the story by talking about base-10 system. When you understand the base-10 system, our story will not be interrupted and confused.
Okay, the base-10 system is the most popular one but it's not unique. Many cultures used different systems in the past, however, today most of them have moved to base-10 system. The base-10 system uses 10 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, which are put together to form another number.
If you only have one box, you can only write a number from 0 to 9. But ..
  • If you have two boxes, you can write a number from 0 to 99.
  • If you have three boxes, you can write a number from 0 to 999.
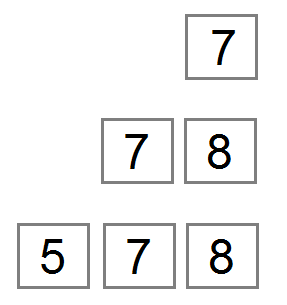
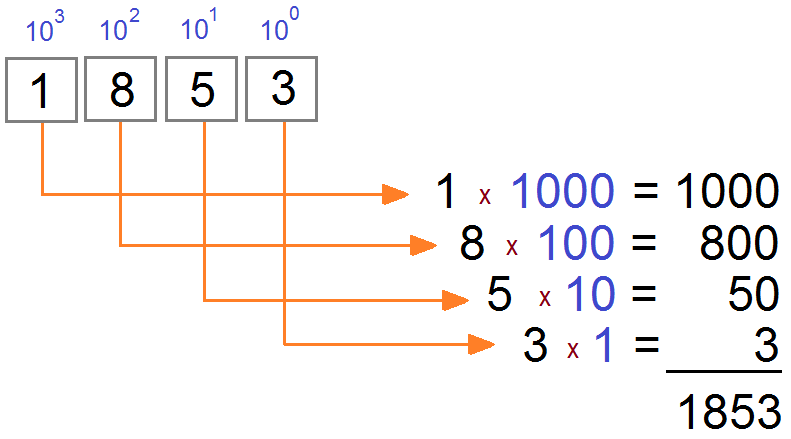
All boxes from right to left have a factor which is in turn 10^0, 10^1, 10^2, ...
BIT
BIT is short for Binary digIT (information unit). A bit that denotes value 0 or 1, is called the smallest unit in the computer. 0, 1 are two basic digits of base-2 system.
Let infer as base-10 system and apply it to base-2 system. If you have one box, you can write 2 numbers such as 0 and 1. If you have 2 boxes, you can write 4 numbers such as 00, 01, 10, and 11 (Note: Do not be mistaken, these numbers are ones of base-2 system).
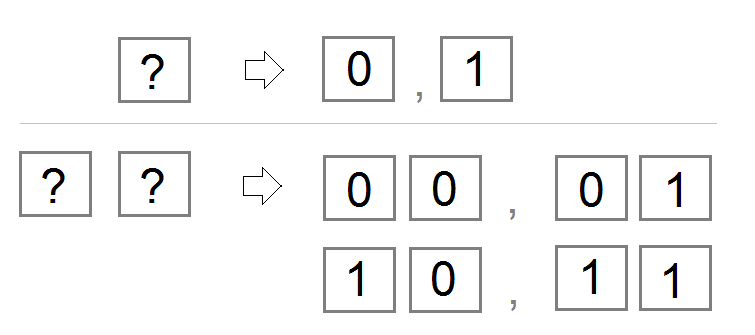
For base-2 system, the boxes from right to left have 1 factor. They are in turn 2^0, 2^1, 2^2, ...
The following image describes the way how to convert a number of base-2 system to base-10 system.
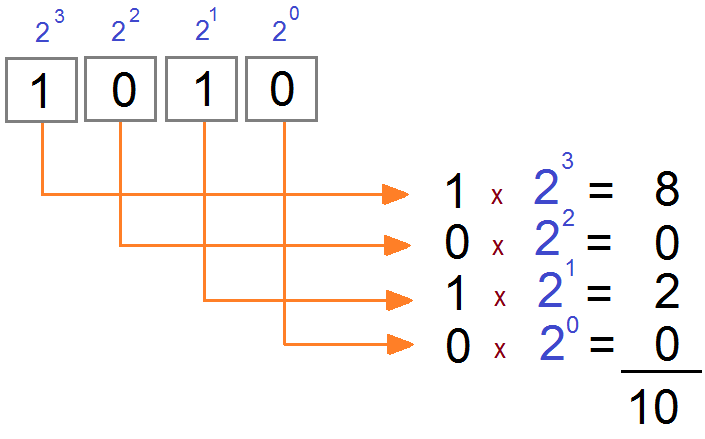
Thus:
  • If you have two boxes in the base-2 system, you can write the largest number of 11 (base-2), which is equivalent to 3 in the base-10 system.
  • If you have 3 boxes in base-2 system, you can write the largest number of 111 (base-2), which is equivalent to 7 in base -10 system.
And you have the following table:
Box Numbers
Maximum Number (Base-2)
Convert to Base-10
1
1
1 (2^1 - 1)
2
11
3 (2^2 - 1)
3
111
7 (2^3 - 1)
4
1111
15 (2^4 - 1)
5
11111
31 (2^5 - 1)
6
111111
63 (2^6 - 1)
7
1111111
127 (2^7 - 1)
8
11111111
255 (2^8 - 1)
9
111111111
511 (2^9 - 1)
Why does the computer use base-2 system but not base-10 system?
You surely ask the question "Why does computer use base-2 system but not base-10 system?". I have asked this question before, like you.
Computers operate by using millions of electronic switches (transistors), each of which is either on or off (similar to a light switch, but much smaller). The state of the switch (either on or off) can represent binary information, such as yes or no, true or false, 1 or 0. The basic unit of information in a computer is thus the binary digit (BIT). Although computers can represent an incredible variety of information, every representation must finally be reduced to on and off states of a transistor.
Thus, the answer is that computer does not have many states to store information, therefore, it stores information based on the two states of ON and OFF (1 and 0 respectively).
Your computer hard drive also stores data on the principle of 0, 1. It includes recorders and readers. It has one or more disks, which are coated with a magnetic layer of nickel. Magnetic particles can have south-north direction or north-south direction, which are two states of magnetic particle, and it corresponds to 0 and 1.
The reader of hard drive can realize the direction of each magnetic particle to convert it into 0 or 1 signals.
The data to be stored on hard drive is a line of 0 or 1 signals. The recorder of hard drive relies on this signal and changes the direction of each magnetic particle accordingly. This is the principle of data storage of hard drive.

2. Byte

Byte is an unit in computer which is equivalent to 8 bits. Thus, a byte can represent a number in range of0 to 255.
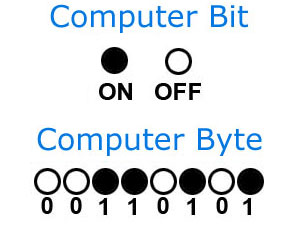
Why is 1 byte equal to 8 bit?
Your question is now "Why is 1 byte equal to 8 bits but not 10 bits?".
At the beginning of computer age people have used baudot as a basic unit, which is equivalent to 5 bits, i.e. it can represent numbers from 0 to 31. If each number represents a character, 32 is enough to use for the uppercase letters such as A, B, ... Z, and a few more characters. It is not enough for all lowercase characters.
Immediately after, some computers use 6 bits to represent characters and can represent at maximum 64 characters. They are enough to use for A, B, .. Z, a, b.. Z, 0, 1, 2, .. 9 but not enough for other characters such as +,-,*, / and spaces.Thus, 6 bits quickly become to be restricted.
ASCII defined a 7-bit character set. That was "good enough" for a lot of uses for a long time, and has formed the basis of most newer character sets as well (ISO 646, ISO 8859, Unicode, ISO 10646, etc.)
ASCII sets:
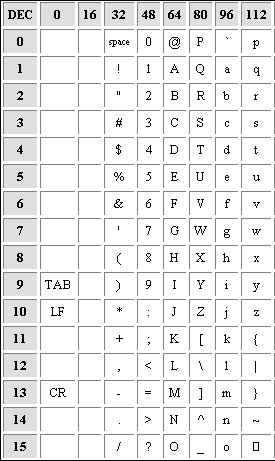
8-bit, a little bit more than 7-bit which is better. It doesn't cause too large waste. The 8-bit is a collection of numbers between 0 and 255 and it satisfies computer designers. The concept of byte was born, 1 byte = 8 bits.
For 8-bit, Designers can define other characters, including special characters in computer. ANSI code table was born which is inheritance of the ASCII code table:
ANSI Sets:
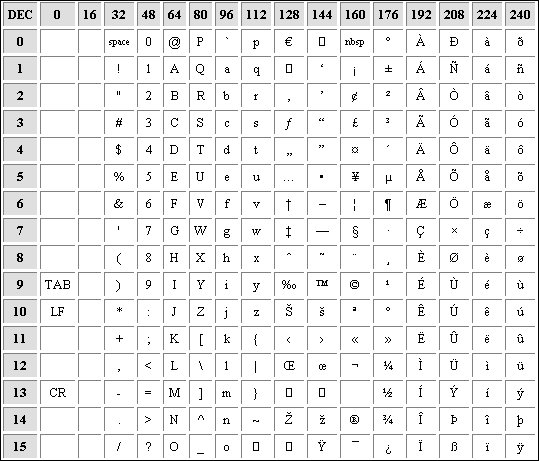
There are many character sets with a view to encoding characters in different languages. For example, Chinese, Japanese require a lot of characters, in which case people uses 2 bytes or 4 bytes to define a character.

Java Basic

Show More

Java Basic

Show More